| I Définitions | |
|
Chiffres et nombres :
Une année comporte douze mois :
douze (12) est un nombre comportant deux chiffres (1 et 2). |
Base : On a pris l'habitude de compter en "paquets". La numération moderne regroupe les éléments à dénombrer en "paquets" de dix. On dit qu'on utilise la "base dix". ex : 2 583 = 2 x 103 + 5 x 102 + 8 x 101 + 3 x 100 Questions : |
| II Deux grands types de numération : | |||
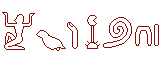
| Numération
additive : La numération égyptienne utilisait les hiéroglyphes ci-contre. Leurs symboles évoquent chacun un ordre de grandeur.
On additionne les valeurs de tous les signes
utilisés pour écrire le nombre. |
Les chiffres :
|
Numération
de position : Un exemple actuel : la numération décimale moderne utilisant les chiffres arabes. La valeur représentée par un chiffre dépend de sa position. 3 344 = 3 x 103 + 3 x 102 + 4 x 101 + 4 x 100 C'est pourquoi on parle de numération de position. On fait ainsi l'économie de l'écriture de nombreux signes. |
Les chiffres :
|
| Q 1 :
Ecrire les nombres 10275 et 2000. Q 2 : Le zéro est-il nécessaire dans ce type de numération ? Q 3 : Faire une phrase pour donner le principe d'une numération additive. Q 4 : Quelle base utilise la numération égyptienne ? D'après vous, pourquoi cette base a-t-elle été souvent choisie dans les numérations inventée par l'homme ? |
Q 5 : Dire simplement, à partir de l'écriture d'un même nombre dans les deux numérations ci-dessus, une raison pour laquelle les numérations de position sont un progrès par rapport aux numérations additives. | ||
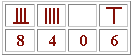
| Numération
romaine : La numération romaine permettait d'écrire les neufs premiers chiffres ainsi :  On remarque l'écriture du chiffre quatre et celle du chiffre
neuf. Ce n'est qu'au Moyen-Age qu'on a écrit les chiffres romains
en utilisant des différences telles que IX (neuf), XC (quatre-vingt
dix)... |
Signes employés : |
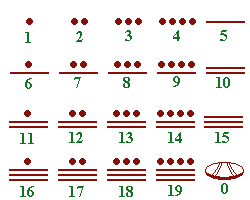
Numération
savante chinoise : Cette numération à base dix était utilisée pour les mathématiques. Elle comporte neuf chiffres, le zéro étant indiqué par une case vide (espace). Il existe deux sortes de chiffres (voir ci-contre) selon le rang. Ainsi, 1987 s'écrit et 2026 s'écrit On pourrait reprocher à ce système
de numération un risque d'erreur, si l'espace est oublié. L'alternance
des deux types de chiffres évite cette ambigüité. Toutefois, le
risque existe si deux zéros se suivent, mais il est impossible de
ne pas remarquer le double espace.
ces abaques ont ensuite disparu. |
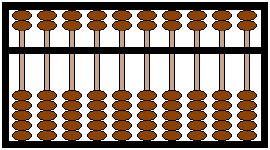
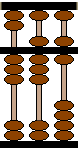
Colonne
1 : chiffres de rangs impairs, utilisés
pour les unités, les centaines, ... Colonne 2 : chiffres de rangs pairs, utilisés pour les dizaines, les milliers, ...
Le boulier permet d'afficher les nombres selon cette même logique. |
| Q 1 :
Ecrire les nombres 1948 et 2001 en numération romaine. Q 2 : Traduire les nombres ci-dessous en numération actuelle. |
Q 3 :
Lire les nombres suivants : Q 4 : Ecrire en numération savante chinoise, les nombres ci-dessous : 3962, 640, 64 et 6400. |
||
| III La numération Maya : la base vingt | ||||||
|
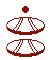
La base vingt
Les Mayas écrivaient leurs nombres de haut en bas :
|
Q 1 : Combien de
signes sont utilisés pour écrire les chiffres de 0 à 19 ? Q 2 : Que représentent les trois nombres ci-après écrits en base vingt ? Rappel : en base dix, 462 = 4 x 102 + 6 x 101 + 2 x 100
|
|||||
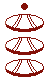
L'influence
du calendrier
La numération maya étant utilisée pour le calendrier, il advint que le nombre représentant une date correspondait exactement aux subdivisions du calendrier. Ainsi, le chiffre d'ordre 3, (ici 7) était à multiplier par 360 au lieu de 400 :
Cette date peut donc être calculée en jours. |
Q 3 : Quel serait
le nombre de jours correspondant à la date ci-contre (à gauche),
si on utilisait réellement la base vingt ?
Q 4 : Quel est le nombre de jours correspondant à cette
date en tenant compte des subdivisions du calendrier maya ? |
|||||
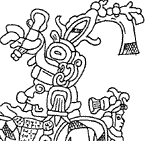
| Un exemple
d'écriture maya (glyphe)
|
||||||
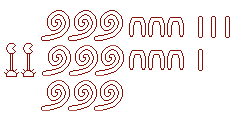
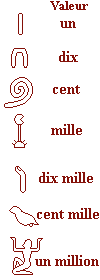


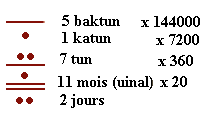
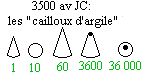
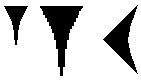
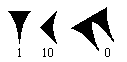
 calame
calame
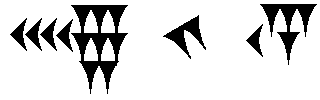



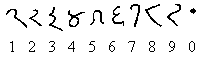
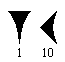

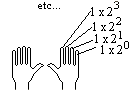 On
utilise alors la base deux.
On
utilise alors la base deux.